1.『〇×相似』とは
難問に出やすい『〇×相似』という相似があります。4番目に出やすい!というわけではないのですが、この考え方を知らないと解けない問題は多いので頭の片隅に置いておきましょう。まずは簡単な直角内直角とも呼べる図形で『〇×相似』を説明します。
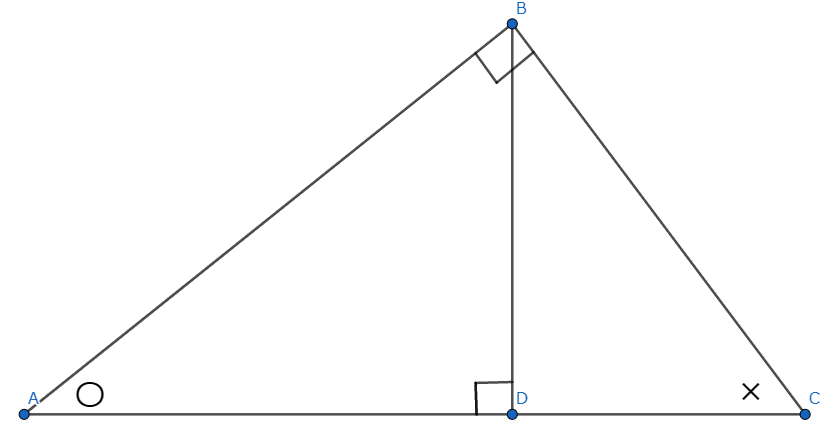
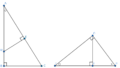
直角三角形の中に直角三角形が入っている形ですね、この形で〇×相似を使う問題は基本問題と言えるでしょう。∠Aを〇、∠Cを×としています。
△ABCの内角の和を考えると
90°+〇+×=180° → 〇+×=90° とわかります。
この『〇+×=90°』を用いるのが『〇×相似』の王道パターンなので、
直角三角形があれば『〇×相似』を意識してください。
ここから△ADBの内角を見てみると、
90°+〇+∠ABD=180° → 〇+∠ABD=90° 〇+×=90°から ∠ABD=× とわかります。
同じように△BDCを考えると∠CBD=〇となるので
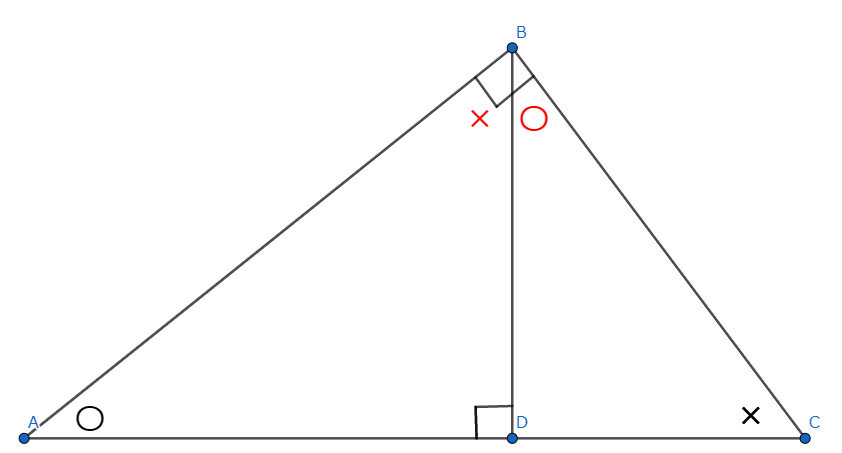
角度が等しいので△ADB∽△BDCとなります。
このように角度の数値がわからなくとも図形の性質から等しい角度を見つけ出し相似を証明するのが『〇×』相似です。証明問題でも解答に少し手間がかかりますので慣れておきましょう。
2.○×相似の頻出問題 折り返し
〇×相似は折り返し問題に出てくることが多いです。
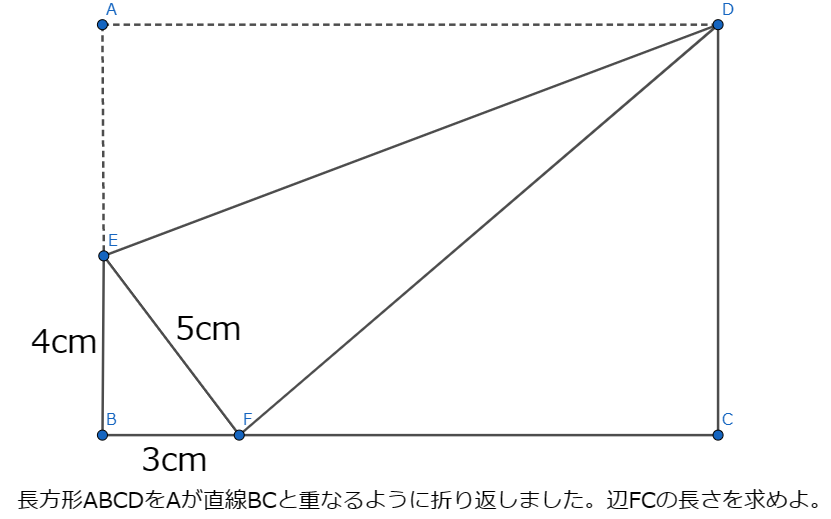
問題
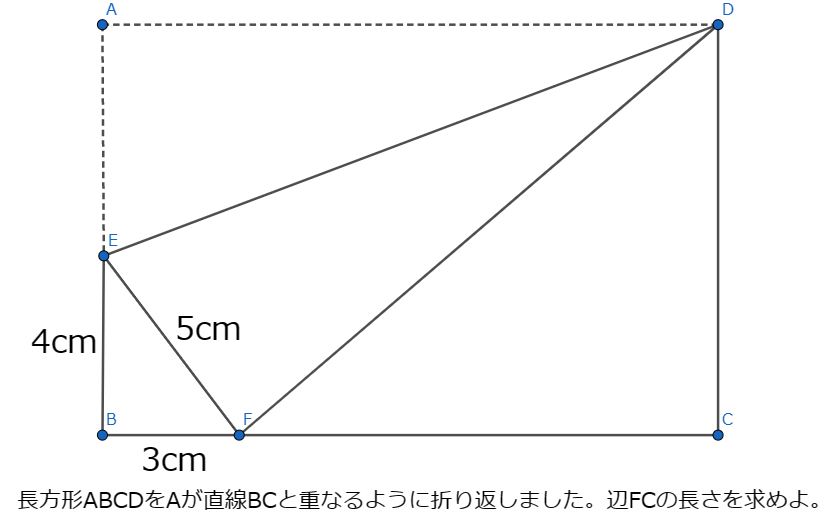
解説
ABCDが長方形なので直角三角形EBFと直角三角形FCDによって作られている∠EFDは∠Aと等しくなり90°とわかります。ここで∠BEFを〇、∠BFEを×とすると〇+×=90°になります。では他に〇や×の角度はないでしょうか。
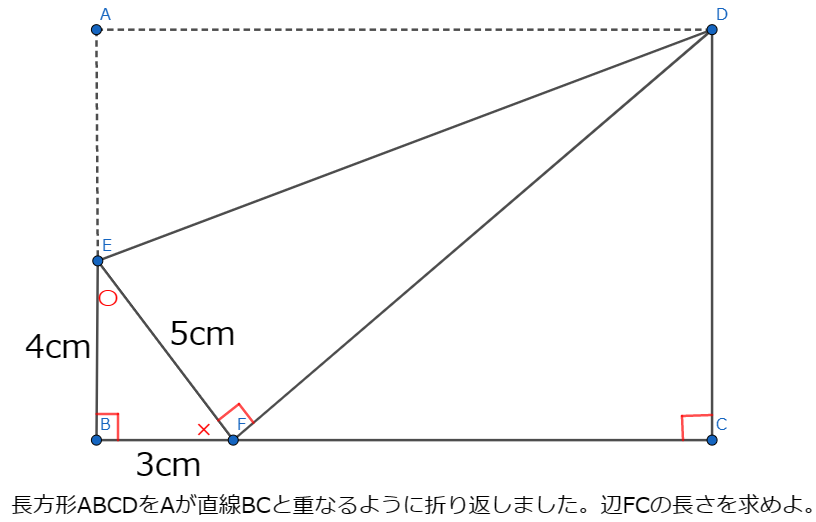
∠BFE・∠EFD・∠DFCは直線を作るので、∠BFE+∠EFD+∠DFC=180°より
×+90°+∠DFC=180° → ×+∠DFC=90° 〇+×=90°より∠DFC=〇とわかります。
これより△EBFと△FCDは2角が等しいので相似となります。(∠CDFは×ですね)
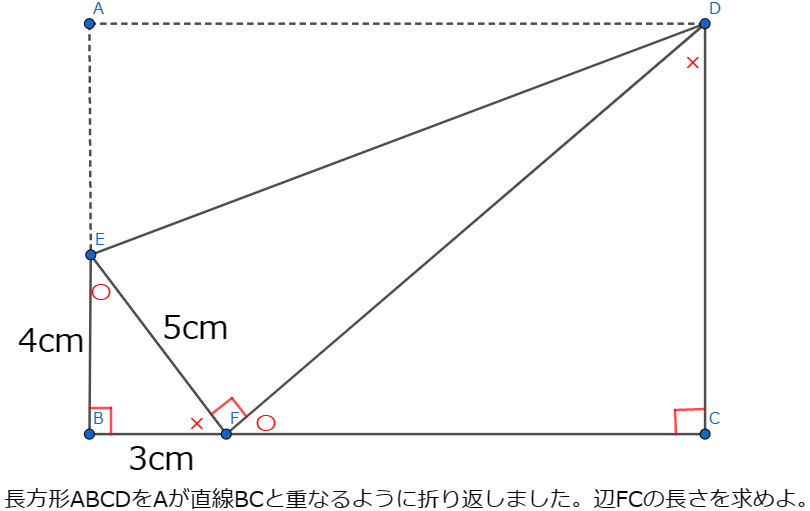
では△EBF∽△FCDを用いて答えを求めましょう。
△EBFの辺の比は4:3:5なので FC:CD:DFも4:3:5となります。
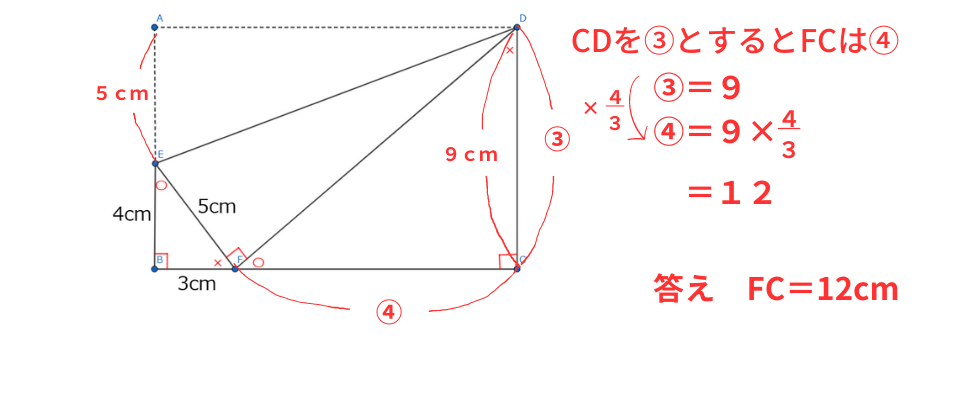
折り返しなのでAE=EF=5cmよりCD=9cmとわかります。
よってFC=9×4/3となり 答えはFC=12cmですね。
難問ででやすいのが〇×相似です。今回扱った問題よりも見つけ辛い問題はたくさんありますので
平面図形で行き詰ったら〇×相似の考え方を思い出してください。


コメント