分数の性質を利用して行う分数倍を習得すれば、受験数学において必須である比の計算を素早く行うことができます。式を書いて計算していた問題も暗算でできるようになるので非常に便利なスキルです。習得難易度は低いので、すぐに使いこなせることでしょう。
1.BはAの何倍か
初めに、ある数が他の数の何倍かを考える時、分数で一瞬で言えるようになりましょう。
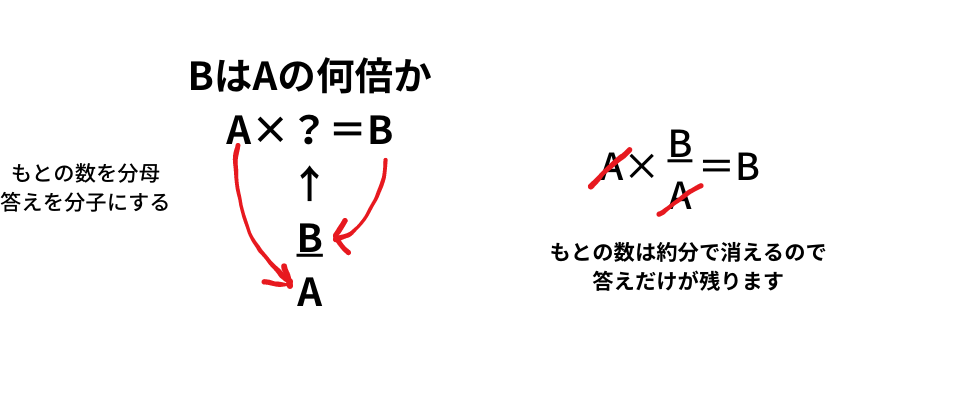
もとの数を分母、答えを分子の考えで次の例題を解いてみてください。
問題
①8は3の何倍か
②159は7の何倍か
③√3は2の何倍か
解説

2.比例式の計算
3:9=□:27のような計算を『内×内=外×外』の公式を使い、9×□=3×27を書いて計算するのは時間の無駄です。分数や小数が絡んだ複雑な問題を除き、比の基本性質と分数倍で答えを求めましょう。比の基本性質を復習しておきます。
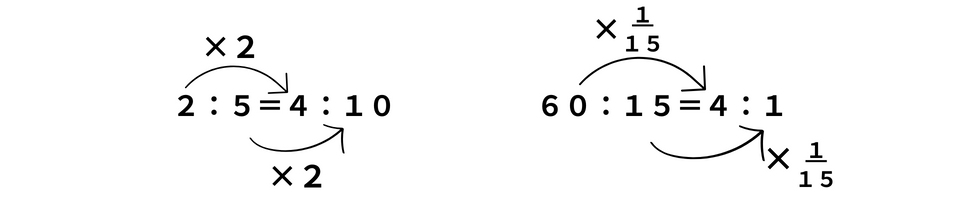
比には、このように同じ数をかけて良いという性質がありますね。
ではこの性質と分数倍を使って先ほどの3:9=□:27を解きましょう。
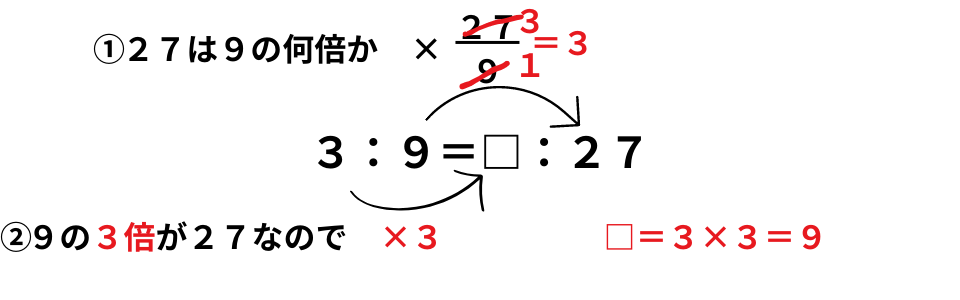
問題
①19:5=□:50
②□:27=11:9
③6:√3=□:8
解説
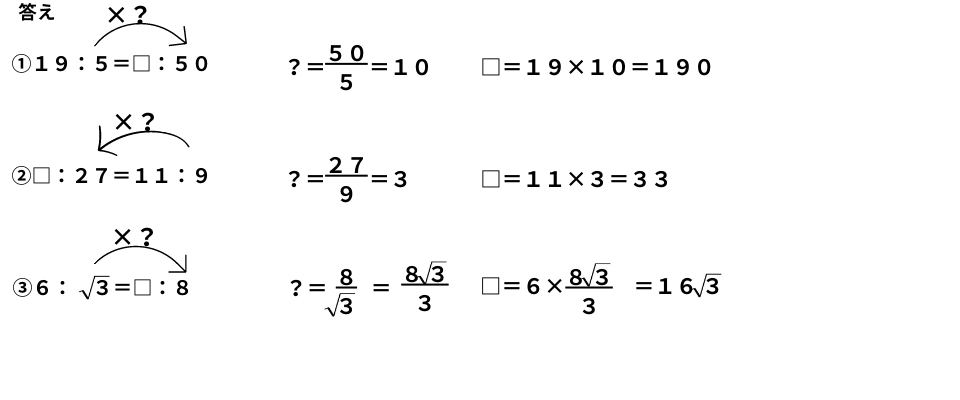
3.図形問題 底⇔面
受験に出てくる図形問題は比を用いる問題ばかりです。分数倍で素早く計算しましょう。まずは底辺の比=面積の比に関する問題です。
問題
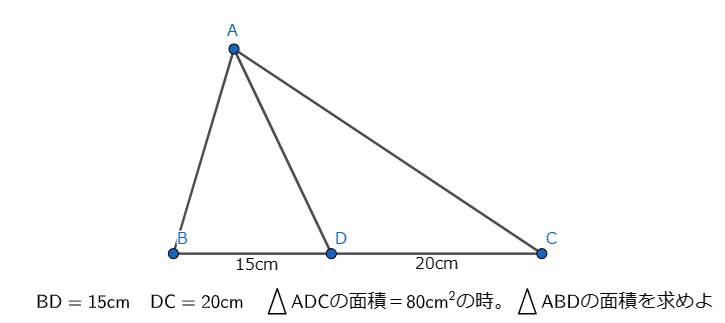
解説
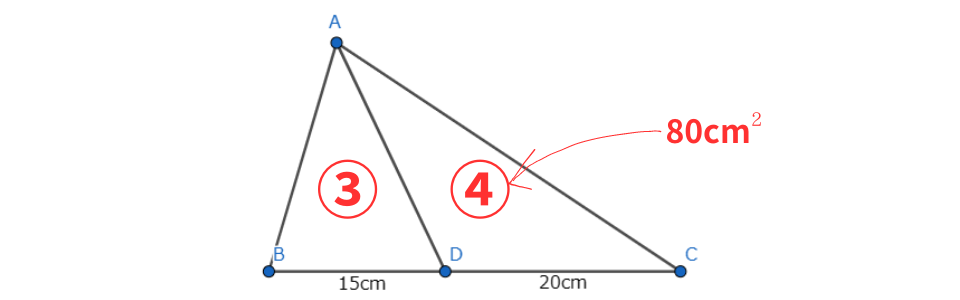
△ABDと△ADCの高さが等しいので、底辺の比=面積の比から
△ADB:△ADC=15:20=3:4となります。
図形問題で比を書きこむときは〇や□などの記号を使いましょう。

4.図形問題 相似
相似は高校受験図形問題の再頻出単元です。
問題

解説
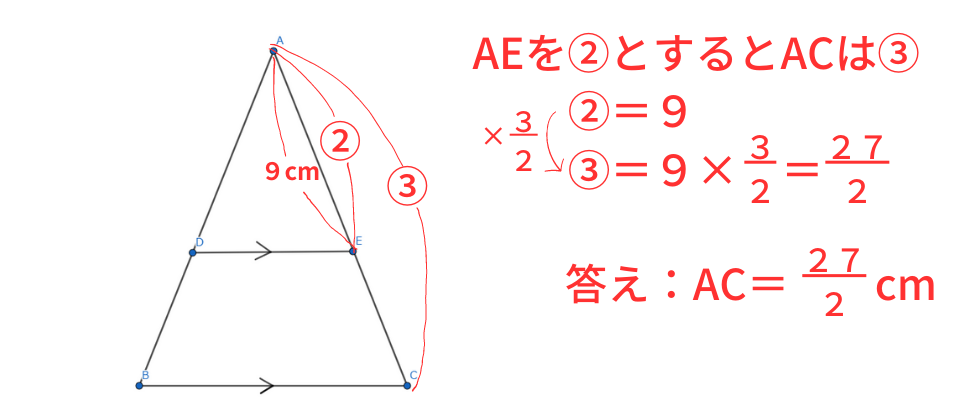
BCとDEが平行なので△ABCと△ADEは相似です。ピラミッド型と呼ばれる形ですね。
対応する辺の比は等しくなるのでAD:AB=AE:ACです。
AD:AB=10:15=2:3なのでAE:ACも2:3とわかります。
では分数倍を用いて答えを求めましょう。
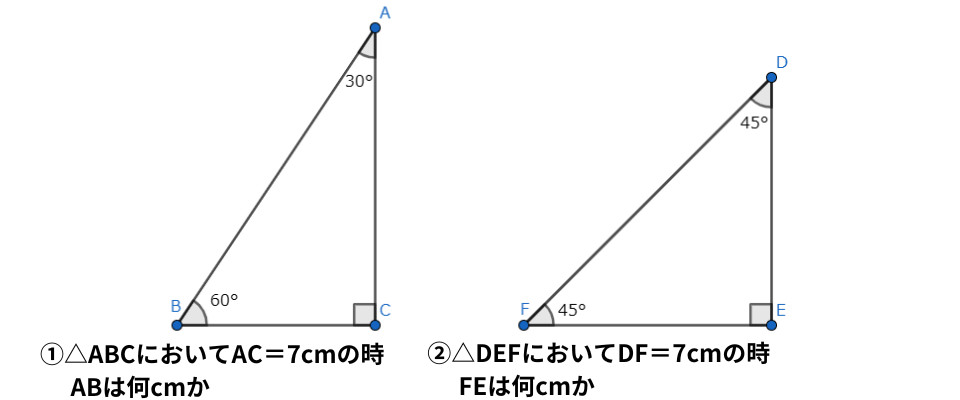
5.図形問題 三角定規の比
2種類の三角定規のそれぞれの長さの比は決まっており、受験では必須の知識です。
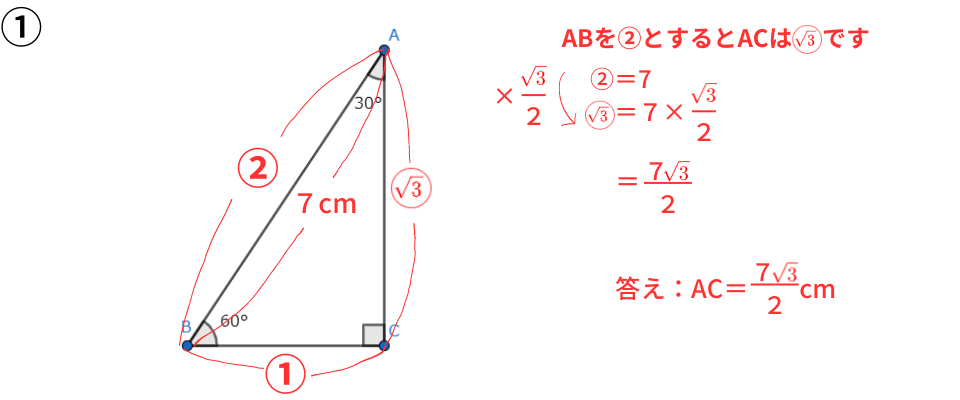
30°・60°の三角定規の三辺の比は1:2:√3
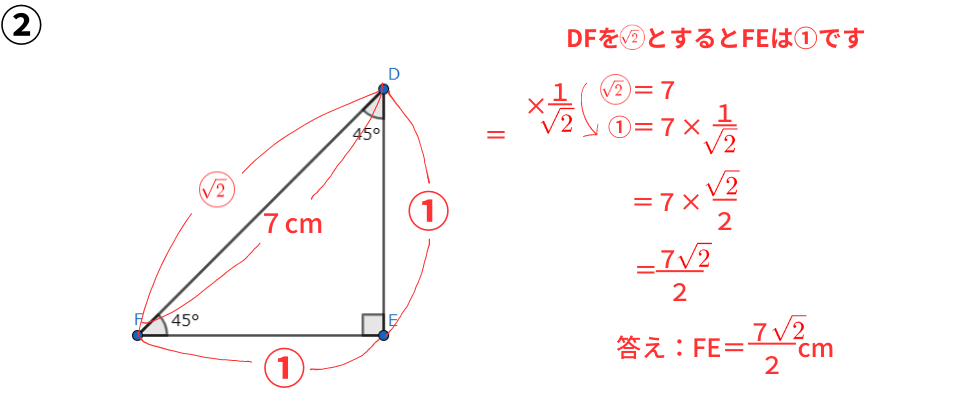
直角二等辺三角の三角定規の三辺の比は1:1:√2となります。
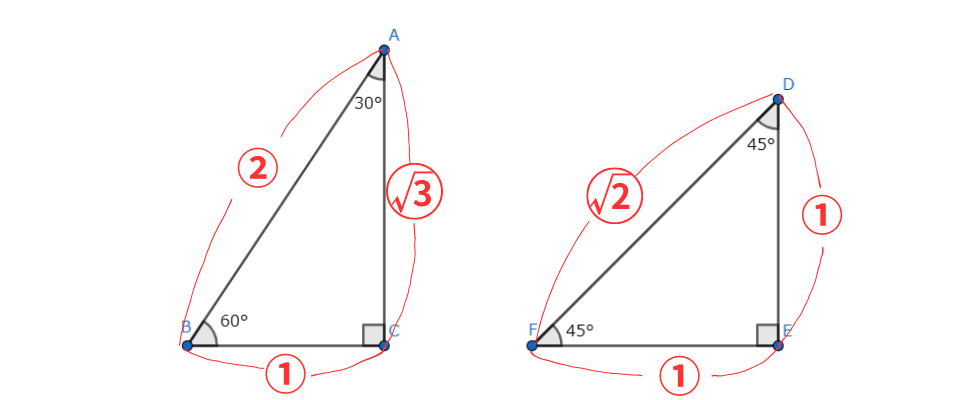
こちらの比を用いた計算も受験頻出なので、分数倍で素早く計算する練習をしておきましょう。
問題
解説


コメント